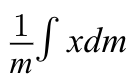Integral Center of Mass

When I took AP Physics C- Mechanics, I had no pre-calculus or calculus experience under my belt beforehand. I walked into the class, and was instantly met with so much trigonometry and calculus. I was a math guy, but with the lack of these skills I was challenged to learn so much in a short amount of time. I was able to skate by for a long time, until I was finally met with the hardest problem I’ve ever faced in my life, the integral method for the center of mass.

The integral center of mass is used to derive the location of the center of mass for objects that may be harder to do through the traditional method. The traditional method, is:

which looks complicated on paper but in practice it's an easy calculation. The x, is the location of an object, and the m, represents the mass of said objects. However, the integral method is where center of mass seems to step it up:

Now, calculus gets involved. Taking the integral of a position with respect to the mass means you have to relate mass and position through the density equation. I feel that explaining it all out here is a waste of time, but as you can see it's a very difficult problem. I consider myself a physics guy, and I consider this to be the hardest problem I’ve ever encountered.

Even though this problem is really difficult, it's so useful for finding the center of mass for objects. Especially for engineers, we need to know the center of mass of objects to better engineer solutions for the object. Its importance is so relevant, so I guess I’ll need to master this skill eventually.